
The electrostatic component was obtained by solving the Poisson-Boltzmann (PB) equation ( 21– 31), and the nonelectrostatic component was obtained based on the solvent-accessible surface area ( 22, 28, 32– 35). The chemical potential of a protein in the solution phase can be written in the form An important advance beyond the previous study ( 20) involves a specific account of the condensed phase. Here we continue our efforts at quantitative predictions of protein solubility. A first step in that direction was taken recently ( 20), and accounted for the effect of salt concentrations on protein solubility by considering electrostatic interactions of salt ions with the charges and the low-dielectric region of a protein in the solution phase, while neglecting the impact of salts in the condensed phase. Of great interest are methods that would predict how protein solubility varies with solvent conditions.
Theoretical models were developed to predict aqueous solubility for drug and druglike compounds ( 16– 19), but developments for proteins are still very limited. Such methods may be used directly to obtain desired levels of solubility for particular proteins, and may provide the necessary guidance for refining experimental techniques to achieve optimal solvent conditions for protein solubility. In addition, charge mutations have been introduced to manipulate the isoelectric point (pI), which is an important determinant of protein solubility ( 12– 15).Īlthough experimental techniques have led to improvements in protein solubility, it is highly desirable to develop theoretical methods for predicting protein relative and absolute solubility. These include time-consuming screening strategies for optimal solvent conditions ( 2, 3), coexpression with molecular chaperones ( 4), attachment of a small protein (fusion tag) ( 5, 6) or peptide (poly-Lys or poly-Arg) ( 7) as a solubility enhancement tag, and rational mutations of surface-exposed hydrophobic residues to polar residues ( 8– 10), as reviewed by Trevino et al. A number of techniques were proposed to increase protein solubility. Low solubility is found to enhance amyloid fibril formation ( 1), and is expected to play a major role in diseases associated with protein aggregation. Most biochemical experiments rely on this ability, such as protein expression and purification, high-resolution structural determination, and quantitative binding assays. This ability is measured by the solubility, i.e., the equilibrium concentration of the protein in the solution phase when a saturation amount of the protein is present. The ability of a protein to dissolve in aqueous solutions is an important property. This study provides valuable insights into the physical basis of protein solubility.
This treatment of electrostatic contributions combined with a similar approach for nonelectrostatic contributions led to a quantitative rationalization of the effects of point mutations on the solubility of ribonuclease Sa.
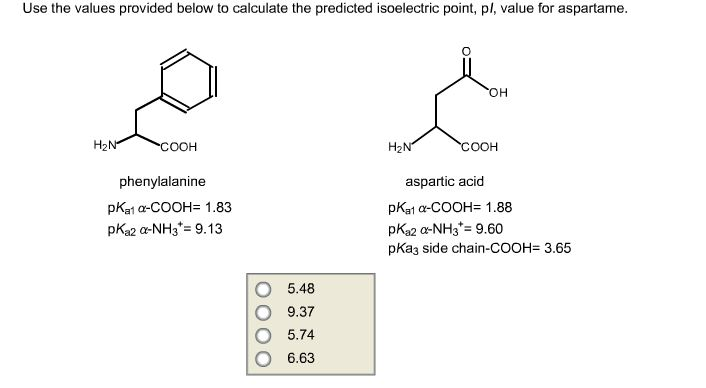
#Calculate pi isoelectric point free
The average transfer free energy from the condensed phase to the solution phase was found to predict reasonably well the variations in solubility of ribonuclease Sa and insulin with pH.
Conformations were then selected for calculations of the electrostatic solvation energy: once for the condensed phase, and once for the solution phase. To account for the effects of pH, the protonation states of titratable side chains were sampled by running constant-pH molecular dynamics simulations. The condensed phase was modeled as an implicit solvent, with a dielectric constant lower than that of water. We studied the effects of pH and mutations on protein solubility by calculating the transfer free energy from the condensed phase to the solution phase. Solubility plays a major role in protein purification, and has serious implications in many diseases.


 0 kommentar(er)
0 kommentar(er)
